| Introduction |
| Publications |
| Download |
Models for CM and PM
We assume now that the system is subjected to both corrective and preventive maintenance, and that PM are done at planned times
![]() . Let
. Let
![]() be the counting process of both kinds of maintenance (PM and CM),
be the counting process of both kinds of maintenance (PM and CM),
![]() be the counting process of PM,
be the counting process of PM,
![]() , be the maintenance times (PM and CM) and
, be the maintenance times (PM and CM) and ![]() be the inter-maintenance times,
be the inter-maintenance times,
![]() for
for ![]() with
with ![]() .
.
An imperfect maintenance model has to be chosen for each kind of maintenance. In MARS, all the combinations between ABAO, AGAN, ARA![]() and ARA
and ARA![]() models are implemented [Doyen and GaudoinDoyen and
Gaudoin2006]. For instance, the ARA
models are implemented [Doyen and GaudoinDoyen and
Gaudoin2006]. For instance, the ARA![]() -ARA
-ARA![]() model assumes that maintenance reduces the virtual age of the system of a quantity proportional to the virtual age just before the maintenance, but the proportional factor is different for PM and CM. If
model assumes that maintenance reduces the virtual age of the system of a quantity proportional to the virtual age just before the maintenance, but the proportional factor is different for PM and CM. If ![]() and
and ![]() denote respectively the PM and CM efficiencies, the failure intensity of the model is shown to be:
denote respectively the PM and CM efficiencies, the failure intensity of the model is shown to be:
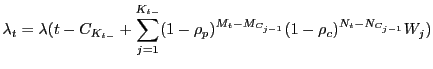 |
(4) |
Stephane Despreaux 2009-06-10
