| Introduction |
| Publications |
| Download |
Models for CM Only
Let
![]() , be the failure times of the system or equivalently the CM times. Let
, be the failure times of the system or equivalently the CM times. Let
![]() , be the inter-failure times, and
, be the inter-failure times, and ![]() be the number of failures up to time
be the number of failures up to time ![]() .
.
![]() is a point process with the following failure intensity:
is a point process with the following failure intensity:
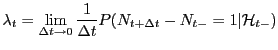 |
(1) |
where
Before the first maintenance, the failure intensity is the hazard rate of a new system. It is denoted
![]() and is called initial intensity. In the following, we assume that the first failure time has a Weibull distribution, i.e. the initial intensity is:
and is called initial intensity. In the following, we assume that the first failure time has a Weibull distribution, i.e. the initial intensity is:
| (2) |
where
The CM models implemented in MARS are the ABAO, AGAN, ARA![]() and ARA
and ARA![]() models [Doyen and GaudoinDoyen and
Gaudoin2004]. In the next version, the Brown-Proschan model [Brown and ProschanBrown and
Proschan1983] will also be available.
models [Doyen and GaudoinDoyen and
Gaudoin2004]. In the next version, the Brown-Proschan model [Brown and ProschanBrown and
Proschan1983] will also be available.
The ARA models are virtual age models. These models consider that, after ![]() maintenance, the system is equivalent to a new one having survived without failure until an age
maintenance, the system is equivalent to a new one having survived without failure until an age ![]() , with
, with
![]() . The virtual age at time
. The virtual age at time ![]() is
is
![]() .
For instance, the ARA
.
For instance, the ARA![]() model assumes that maintenance reduces the virtual age of the system of a quantity proportional to the virtual age just before the maintenance. This quantity is denoted
model assumes that maintenance reduces the virtual age of the system of a quantity proportional to the virtual age just before the maintenance. This quantity is denoted ![]() and characterizes maintenance efficiency. Thus, the failure intensity of the system is:
and characterizes maintenance efficiency. Thus, the failure intensity of the system is:
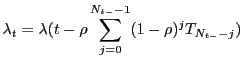 |
(3) |
Basic models are particular cases of the ARA![]() model, according to the values of
model, according to the values of ![]() :
:
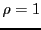 : perfect maintenance (AGAN),
: perfect maintenance (AGAN),
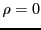 : minimal maintenance (ABAO),
: minimal maintenance (ABAO),
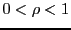 : imperfect but efficient maintenance,
: imperfect but efficient maintenance,
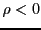 : harmful maintenance.
: harmful maintenance.
Stephane Despreaux 2009-06-10
